종종 센서 데이터(또는 신호)를 이용하여 작업하는 동안 데이터가 깨끗하지 않고 상당한 양의 노이즈를 나타내는 경우가 많다. 이러한 노이즈는 추가 수학적 연산을 수행하기 어렵게 만든다. 또한, 노이즈는 다운스트림 수학 연산에서 증폭되는 경향이 있으므로 자율주행차량, 우주로켓, 로봇 팔 또는 산업 플랜트 제어와 같은 실시간 작업에 이러한 신호를 사용하려는 경우 큰 문제가 될 수 있다.
이런 경우 한 가지 일반적인 접근 방법은 데이터를 평활화하여 노이즈를 제거하는 것이다. 다시말해 자율주행차량이나 로봇 제어와 같은 제어 엔지니어링의 응용 프로그램을 위해 이러한 데이터를 실시간으로 평활화하려고 한다. 칼만 필터, 확장 칼만 필터 및 그 변형과 같이 실시간 방식으로 신호를 부드럽게 하기 위한 여러 방법이 이미 개발되었다. 그러나 Kalman 필터를 설계하려면 알려지거나 알려지지 않은 시스템 역학에 대한 지식이 필요하다. 이러한 상황에서 더 간단한 접근 방식은 수신된 마지막 n개의 데이터 포인트의 최소제곱 다항식 피팅을 수행하는 것이다. 다항식 회귀는 비선형 관계를 점 집합에 맞추는 것을 목표로 한다.
예를 들어 자동차 속도센서의 출력값으로 다음과 같은 데이터를 생각해보자.
velocity:
일반적으로 이런 데이터들은 알아보기 쉽지않으므로 시각화를 해야한다. 여기서는 Qt 프레임워크 및 Qwt 라이브러리를 이용하여 플롯 할 것이다. 시간에따는 속도 변화량을 다음과 같이 시각화할 수 있다.
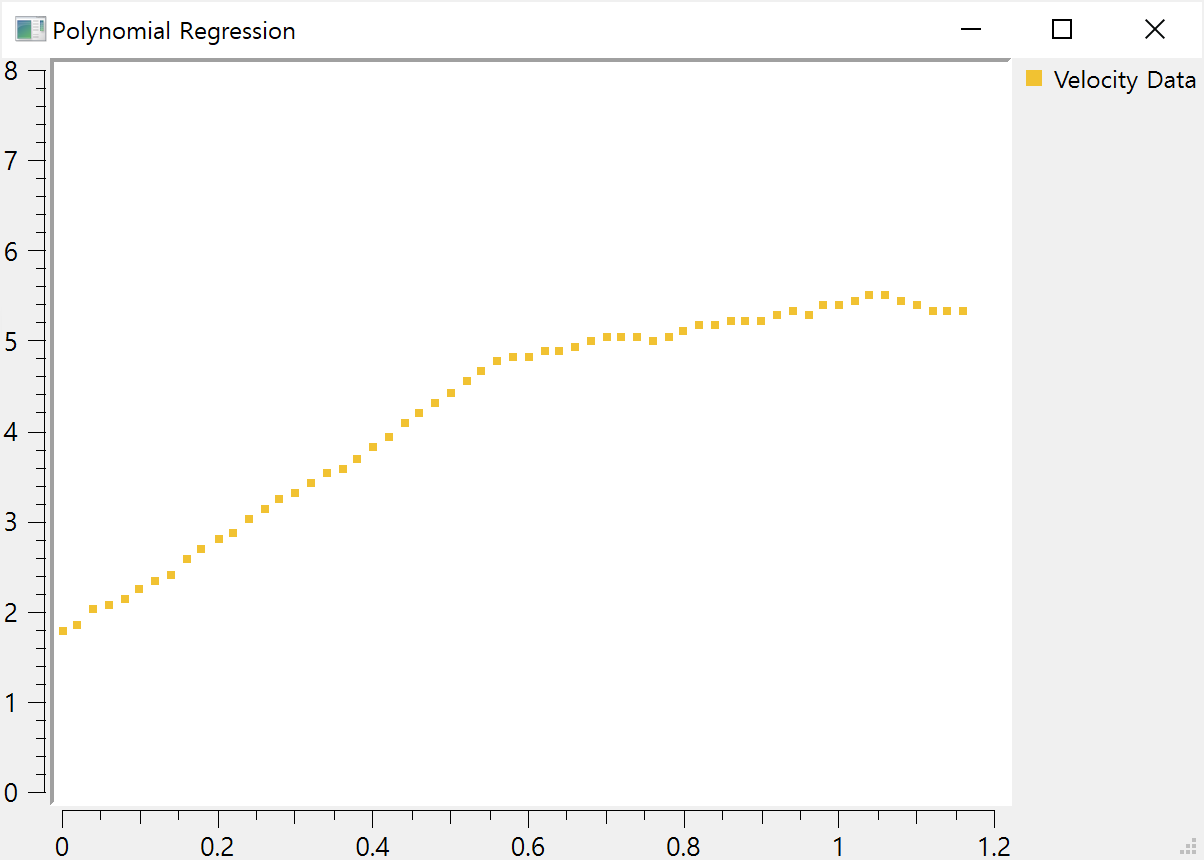
이 결과가 어느정도 괜찮아 보일 수 있겠으나 위에서도 언급했듯이 안전과 밀접하게 관련된 실시간 시스템에서 의도하지않은 문제를 초래할 수도 있다.
기본적인 최소제곱 다항식 피팅의 수학은 다음과 같다.
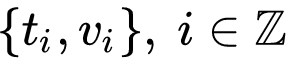
차수 k의 다항식 피팅은 다음과 같이 쓸 수 있다.
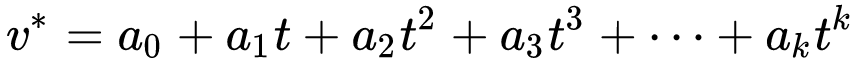
이 경우의 나머지는 다음과 같이 주어진다.
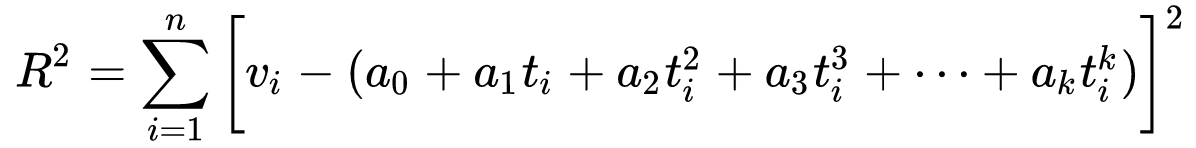
최소제곱 다항식 피팅의 목적은 R² 를 최소화하는 것 이다. 일반적인 접근 방식은 계수 a에 대해 방정식 2의 편미분을 취하고 0과 같다. 이것은 k 방정식의 시스템으로 이어진다. 이러한 방정식 시스템은 다음과 같이 단순화된 Vandermonde 행렬 방정식으로 나타낸다.
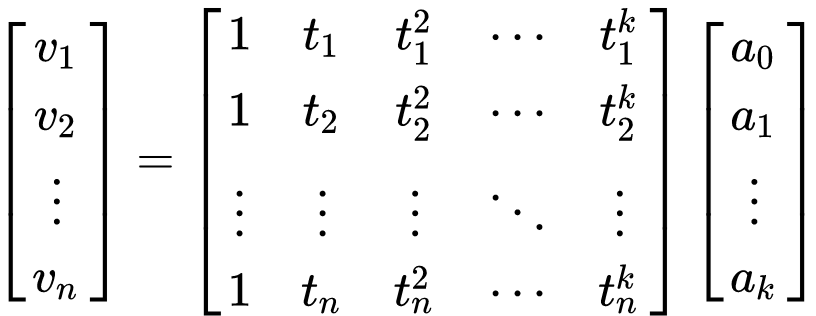
위의 행렬 표기법에서 다음과 같이 쓸 수 있다.
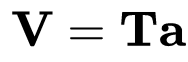
T 의 전치를 미리 곱하여 풀 수 있으므로 솔루션 벡터는 다음과 같다.
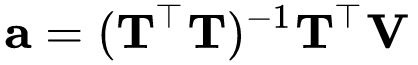
Eigen 라이브러리를 이용하여 위 식을 쉽게 풀 수 있다. 다음은 이 문제에 대한 핵심부분을 보여주기 위한 주요코드이다. 여기서는 3차 다항식으로 맞춘다. 더 높은 차수의 다항식을 맞추는 것은 계산 비용이 많이 들고 전혀 필요하지 않을 수 있다.
#include <iostream>
#include <cmath>
#include <vector>
#include <Eigen/Dense>
#include <Eigen/QR>
void polyfit( const std::vector<double> &t,
const std::vector<double> &v,
std::vector<double> &coeff,
int order )
{
// Create Matrix Placeholder of size n x k, n= number of datapoints, k = order of polynomial, for exame k = 3 for cubic polynomial
Eigen::MatrixXd T(t.size(), order + 1);
Eigen::VectorXd V = Eigen::VectorXd::Map(&v.front(), v.size());
Eigen::VectorXd result;
// check to make sure inputs are correct
assert(t.size() == v.size());
assert(t.size() >= order + 1);
// Populate the matrix
for(size_t i = 0 ; i < t.size(); ++i)
{
for(size_t j = 0; j < order + 1; ++j)
{
T(i, j) = pow(t.at(i), j);
}
}
std::cout<<T<<std::endl;
// Solve for linear least square fit
result = T.householderQr().solve(V);
coeff.resize(order+1);
for (int k = 0; k < order+1; k++)
{
coeff[k] = result[k];
}
}
int main()
{
// time value
std::vector<double> time = {0, 0.0192341804504395, 0.0394501686096191, 0.059575080871582, 0.0790810585021973, 0.0792751312255859, 0.0987141132354736, 0.119336366653442, 0.138712167739868, 0.159000158309937, 0.178890228271484, 0.19960618019104, 0.219112157821655, 0.23919415473938, 0.259442090988159, 0.279186248779297, 0.299112319946289, 0.319219350814819, 0.339494228363037, 0.339675188064575, 0.359552145004272, 0.37941837310791, 0.399189233779907, 0.419828176498413, 0.439810276031494, 0.459331274032593, 0.479461193084717, 0.499663114547729, 0.519809246063232, 0.539092063903809, 0.559118270874023, 0.579315185546875, 0.598889112472534, 0.619685173034668, 0.638863086700439, 0.639052152633667, 0.658920288085938, 0.679149150848389, 0.699787139892578, 0.71905517578125, 0.73898720741272, 0.739143371582031, 0.758654117584229, 0.779210329055786, 0.799195289611816, 0.819046258926392, 0.839539289474487, 0.85923433303833, 0.87903618812561, 0.899263143539429, 0.919251203536987, 0.939138174057007, 0.959244251251221, 0.979074239730835, 0.998935222625732, 1.01904726028442, 1.0387852191925, 1.03895926475525, 1.05906510353088, 1.07873225212097, 1.09908628463745, 1.11907029151917, 1.13899827003479, 1.15879201889038};
// velocity value
std::vector<double> velocity = {1.8, 1.86, 2.03, 2.08, 2.14, 2.14, 2.25, 2.36, 2.42, 2.59, 2.7, 2.81, 2.87, 3.04, 3.15, 3.26, 3.32, 3.43, 3.54, 3.54, 3.6, 3.71, 3.83, 3.94, 4.11, 4.22, 4.33, 4.44, 4.56, 4.67, 4.78, 4.84, 4.84, 4.89, 4.89, 4.89, 4.95, 5.01, 5.06, 5.06, 5.06, 5.06, 5.01, 5.06, 5.12, 5.18, 5.18, 5.23, 5.23, 5.23, 5.29, 5.34, 5.29, 5.4, 5.4, 5.46, 5.51, 5.51, 5.51, 5.46, 5.4, 5.34, 5.34, 5.34};
// placeholder for storing polynomial coefficient
std::vector<double> coeff;
polyfit(time, velocity, coeff, 3);
std::vector<double> fitted_velocity;
std::cout<< "Printing fitted values" << std::endl;
for(int p = 0; p < time.size(); ++ p)
{
double vfitted = coeff[0] + coeff[1]*time.at(p) + coeff[2]*(pow(time.at(p), 2)) +coeff[3]*(pow(time.at(p), 3)) ;
std::cout<< vfitted<<", ";
fitted_velocity.push_back(vfitted);
}
std::cout<<std::endl;
return 0;
}
다음의 이미지는 이 문제의 결과를 시각화한 것이다.
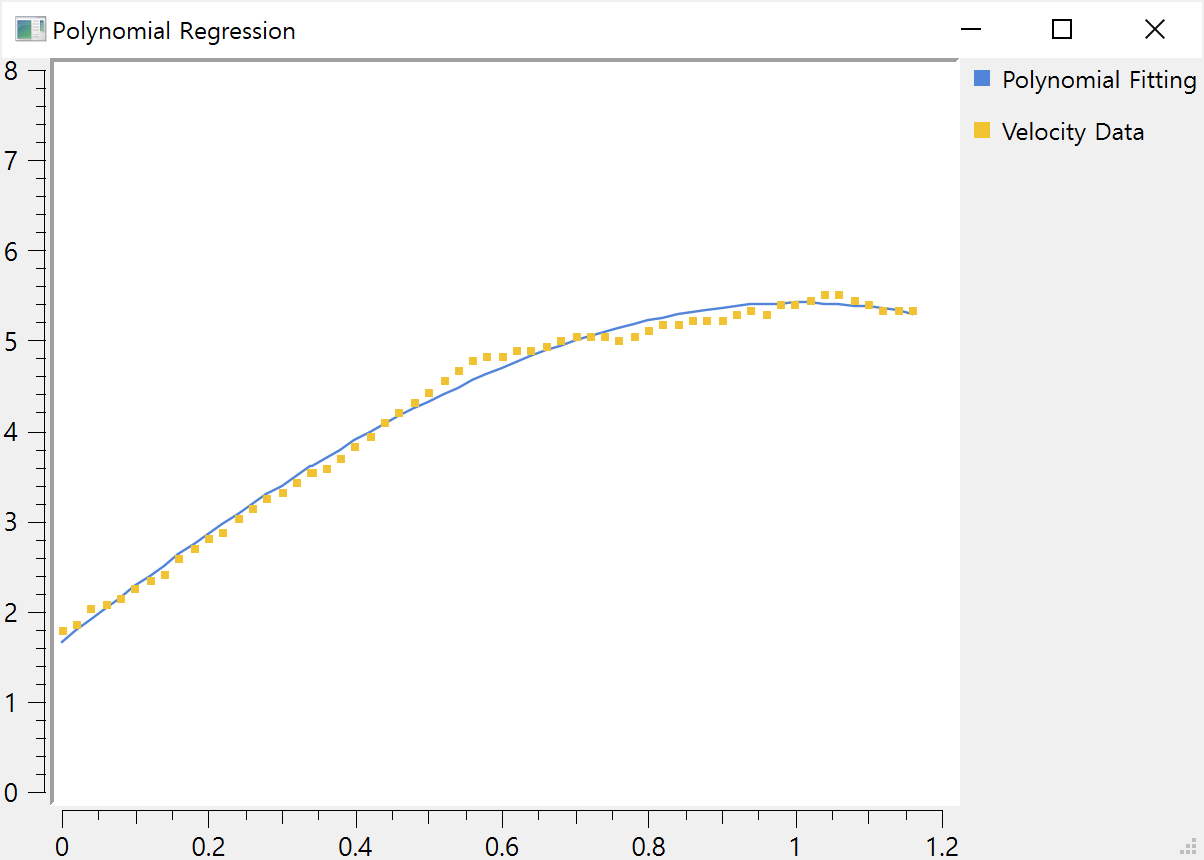
각각의 데이터를 통과하지않고 그 일반적인 형태나 경향에 결합시키는 것을 알 수 있다.