원 그래프를 그리는 것 중, 세 점을 지나는 원을 그리는 내용이다. 먼저 점 3개가 주어졌다고 하자.
이 때, 이 세 점을 지나는 원의 중점은 다음 그림과 같이 두 점씩을 이은 선의 수직 이등분선의 교점이 된다. 이 때, 연결선은 임의의 두 점을 선택해도 무방하다.
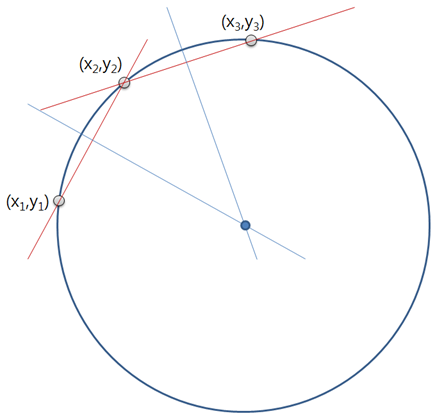
여기서는 위와 같이 연결선을 만들었다고 가정한다.
/**
@brief 세점을 지나는 원의 중심점과 반지름을 구한다.
@param * r: 원의 반지름
@param * psRelMatchPos: 원의 중심점 좌표
@param * psCenterPoint: 세점들의 좌표
@return Error code
*/
ATF_ERR_T CiADAS_ReconstructorDlg ::Get_Three_Point_Circle(float* r, AT_FPOINT* psRelMatchPos, const AT_FPOINT* psCenterPoint)
{
float d1 = (psCenterPoint[1].x - psCenterPoint[0].x)/(psCenterPoint[1].y - psCenterPoint[0].y);
float d2 = (psCenterPoint[2].x - psCenterPoint[1].x)/(psCenterPoint[2].y - psCenterPoint[1].y);
float cx = ((psCenterPoint[2].y - psCenterPoint[0].y) + (psCenterPoint[1].x + psCenterPoint[2].x) * d2 - (psCenterPoint[0].x + psCenterPoint[1].x) * d1)/(2 * (d2 - d1));
float cy = (-d1 * (cx-(psCenterPoint[0].x + psCenterPoint[1].x)/2) + (psCenterPoint[0].y + psCenterPoint[1].y)/2 );
psRelMatchPos->x = cx;
psRelMatchPos->y = cy;
*r = sqrt(pow((float)(psCenterPoint[0].x - cx), 2) + pow((float)(psCenterPoint[0].y - cy), 2));
return ATF_ERR_NONE;
}