1. 원주 흔들림공차의 적용 예
그림 M4-1은 캐스터의 축에 원통도공차와 원주 흔들림공차를 적용한 예이다. 캐스터의 바퀴와 억지 끼워맞춤하는 Ø22mm 원통 부분이 원주 흔들림공차에 의해 규제되고 있다.
그림 M4-1 (나)는 (가)의 해석이다. 이해하기 쉽도록 공차 영역을 과장되게 그렸다. 캐스터의 축을 데이텀 축선(A-B)을 중심으로 1회전시켰을 때 그 표면이 두 개의 동심원을 벗어날 정도로 흔들리면 안 된다는 의미이다. (나)에서 가상선으로 표시된 두 동심원의 반지름의 차이(0.011)는 공차와 같고 이들 두 개의 동심원으로 만들어지는 도넛(donut)이 공차 영역이다. 두 동심원의 중심은 축의 중심과 같다. 원주 흔들림 공차는 축의 치수와 관계없이 적용된다.
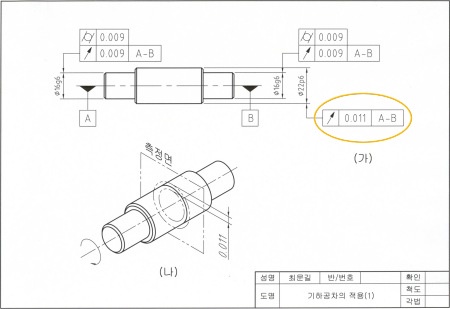
<그림 M4-1>
2. 원통도공차의 적용 예
그림 M4-2는 캐스터의 부시에 원통도공차와 원주 흔들림공차를 적용한 예이다. 원통도공차가 지시된 Ø16mm 구멍은 축과 헐거운 끼워맞춤으로 조립되어 회전운동을 하는 부분이며, 동시에 원주 흔들림공차의 데이텀(C)이다. 원통도공차는 데이텀을 필요로 하지 않는다.
그림 M4-2 (나)는 (가)의 해석이다. 이해하기 쉽도록 공차 영역과 구멍의 표면을 과장되게 그렸다. 부시 구멍의 모든 표면이 두 동심원 사이에 들어갈 정도로 정밀한 원통이어야 한다는 의미이다.
(나)에서 가상선으로 그려진 두 개의 동심원이 만드는 도넛이 공차 영역이며, 두 동심원의 반지름의 차이가 공차(0.009)와 같다. 두 동심원의 중심은 구멍의 중심과 같다.
원통도공차는 직진도진원도평행도공차를 동시에 적용한 것과 같으며, 구멍의 치수와 관계없이 적용된다.
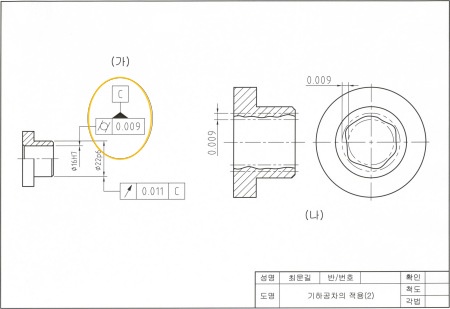
<그림 M4-2>
표 M4-1은 일반적으로 적용하는 기하공차의 공차 영역을 나타낸 것이다.
기어는 기하공차와 공차 영역이 KS에 규정되어 있다.
| 적용하는 기하공차 | 정밀 | 보통 | 거침 | 데이텀 | |
| 모양 | 직진도공차 | 0.02/1000 | 0.05/1000 | 0.1/1000 | 필요 없다 |
| 0.01 | 0.05 | 0.1 | |||
| Ø0.02 | Ø0.05 | Ø0.1 | |||
| 평면도공차 | 0.02/100 | 0.05/100 | 0.1/100 | ||
| 0.02 | 0.05 | 0.1 | |||
| 진원도공차 | 0.005 | 0.02 | 0.05 | ||
| 원통도공차 | 0.01 | 0.05 | 0.1 | ||
| 선의 윤곽도공차 | 0.05 | 0.1 | 0.2 | ||
| 면의 윤곽도공차 | 0.05 | 0.1 | 0.2 | ||
| 자세 | 평행도공차 | 0.01 | 0.05 | 0.1 | 필요하다 |
| 직각도공차 | 0.02/100 | 0.05/100 | 0.1/100 | ||
| 0.02 | 0.05 | 0.1 | |||
| Ø0.02 | Ø0.05 | Ø0.05 | |||
| 경사도공차 | 0.025 | 0.05 | 0.1 | ||
| 위치 | 위치도공차 | 0.02 | 0.05 | 0.1 | |
| Ø0.02 | Ø0.05 | Ø0.1 | |||
| 동축도공차 | 0.01 | 0.02 | 0.05 | ||
| 대칭도공차 | 0.02 | 0.05 | 0.1 | ||
| 흔들림 | 원주·온 흔들림공차 | 0.01 | 0.02 | 0.05 | |
| <표 M4-1> |
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 40 | 표면 경화강과 열처리 경도 | Pjk | 2011.12.29 | 17887 |
| 39 |
재료의 비중표
| Pjk | 2011.12.29 | 29982 |
| 38 | 연삭가공면의 3가지 손상에 대해 | Pjk | 2011.06.16 | 25996 |
| 37 | 절삭가공에서 진동의 종류와 원인 | Pjk | 2011.06.16 | 31092 |
| 36 | 절삭칩의 네가지형태 | Pjk | 2011.06.16 | 26824 |
| 35 |
기계도면 질문좀할께요
| 공학도 | 2011.05.18 | 24871 |
| 34 |
솔리드 모델링 - 자전거 모델링하기
| jkp1985 | 2011.03.31 | 28281 |
| 33 | 기계부품의 재질(재료) 선정 | jkp1985 | 2011.03.24 | 31270 |
| » |
기하공차의 적용
| Pjk | 2011.03.06 | 25029 |
| 31 |
기하공차의 종류
| Pjk | 2011.03.06 | 36480 |
| 30 | 볼트의 기계적 성질 | Pjk | 2011.02.20 | 25047 |
| 29 |
PID제어기_1차시스템설계
[1] | Pjk | 2010.12.16 | 25096 |
| 28 |
서보모터설계 및 기술자료
| Pjk | 2010.12.01 | 25051 |
| 27 |
엔드밀 가공에서 절삭조건이 절삭동력에 미치는 영향
| Pjk | 2010.11.29 | 19470 |
| 26 |
공학도를 위한 수치해석 - 연습문제 chapter 1~25
[3] | Pjk | 2010.10.15 | 25079 |
| 25 |
다듬질 기호와 표면거칠기 기입법
| Pjk | 2010.09.13 | 40588 |
| 24 |
벤추리관(Venturi tube)에 흐르는 유체의 유량
| Pjk | 2010.06.28 | 56298 |
| 23 |
연삭 숫돌의 구성요소, 선택 방법
| Pjk | 2010.06.18 | 25032 |
| 22 |
원판 클러치의 전달토크
| Pjk | 2010.06.13 | 25182 |
| 21 |
Matlab을 이용하여 모터 위치제어를위한 PID제어기 설계
[8] | Pjk | 2010.06.09 | 40879 |