근궤적법(W.R.Evans,1948)
제어시스템내의 어떤 한 계수 값 변화에 따른 폐로시스템의 극점의 위치를 그림으로 나타냄으로써 시스템의 안전성과 성능을 함께 조사하는 방법이며 주로 3차시스템 이상을 다루기위해 이용된다. (여기서는 Matlab을 이용)
근궤적(root locus)
미정계수를 포함하는 특성방정식에서 미정계수 K가 0부터 ∞까지 변할때, 특성방정식의 근이 변화하는 궤적을 복소평면에 그림으로 나타낸것
근궤적의 작성
루프전달함수 KG(s)H(s)를 이용하여 작성
근궤적의 기본성질
1)근궤적의 수
특성방정식의 근(폐루프 극점)의 개수와 같다.
2)근궤적의 출발점과 종착점
-출발점(K=0일때): G(s)H(s)의 극점에서 출발, D(s)=0의 근
-종착점(K=∞일때): G(s)H(s)의 영점에 종착, N(s)=0의 근
3)실수축상의 근궤적
G(s)H(s)의 극점과 영점이 실수축상에 있을때
임의의 구간에서 오른쪽에 있는 극점과 영점을 합한 개수가 홀수이면 그 구간에 근궤적이 존재하고, 짝수이면 근궤적이 존재하지않음.
4)근궤적선도의 대칭성
특성방정식의 복소근은 공액복소수로 존재하므로 실수축에 대하여 대칭을 이룬다.
5)점근선의 각도와 위치
-K가 ∞로 점근할때 근궤적은 점근선(asymptote)을 가짐.
-점근선의 개수: G(s)H(s)의 극점수 n과 영점수 m이 같지 않을때, 점근선의 개수 =n - m
(예제1) 점근선의 각도와 위치
|
K(s+3) G(s)H(s) = ㅡㅡㅡㅡㅡㅡㅡㅡㅡ s(s+1)(s+2)(s+4) |
근궤적작성
>>num=[1,3];den=conv([1,1,0],[1,6,8]);sys=tf(num,den);rlocus(sys)
다음과 같은 근궤적을 확인할 수 있다.
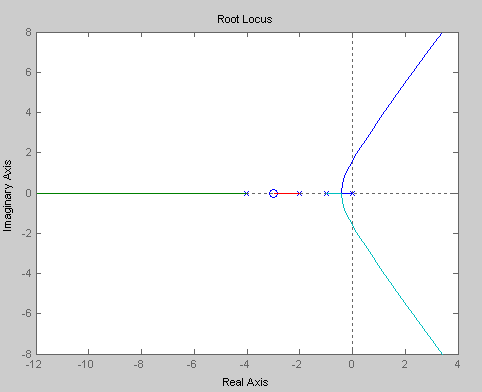
예제1의 2차시스템 응답특성
>>wn=0.69;z=0.508;num=wn^2;den=[1,2*z*wn,wn^2]; t=0:0.01:20; step(num,den,t)
6)출발점과 종착점의 결정하는 각도
-위상조건으로 결정
7)절점의 위치
-절점(break point):특성방정식의 다중근에 대응
이탈점(breakaway point):근궤적이 실수축을 떠나는 점
복귀점(breakin point):근궤적이 실수축에 도착하는 점
8)허수축 교차점
-의미: 안정성의 임계점, 제어시스템의 해석 및 설계에 중요하게 작용된다.
계산법1:특성방정식에서 s값에 ϳω를 대입하여구함(허수축 교차점의 주파수 ω와 근궤적 계수 K를 구할 수 있음)
계산법2:Routh안정성 판별법 이용
(예제2)허수축 교차점
|
1 G(s)H(s) = ㅡㅡㅡㅡㅡㅡㅡㅡㅡ s(s+4)(s²+8s+42) |
근궤적작성
전달함수 다항식계산
>>conv([1,4,0],[1,8,42])
ans =
1 12 74 168 0
>>num=[1];den=[1,12,74,168,0];rlocus(num,den)
예제2의 근궤적
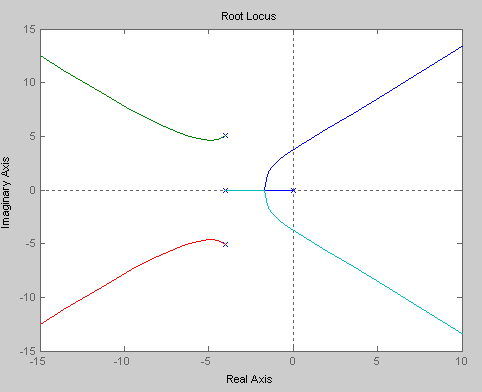
예제2의 2차시스템 응답특성
>>wn=2.16;z=0.681;num=wn^2;den=[1,2*z*wn,wn^2]; t=0:0.01:4; step(num,den,t)
2차응답특성비교과 4차시스템비교
>> w1=2.16;z1=0.681;num1=w1^2;den1=[1,2*z1*w1,w1^2]; t=0:0.01:4; step(num1,den1,t)
>> hold on
>> w2=6.53;z1=0.693;num2=w2^2;den2=[1,2*z2*w2,w2^2]; t=0:0.01:4; step(num2,den2,t)
>> num=num1*num2; den=conv(den1,den2); step(num,den,t)
>> legend('sys1','sys2','sys1+sys2')
| 번호 | 제목 | 글쓴이 | 날짜 | 조회 수 |
|---|---|---|---|---|
| 20 |
수동식 wintch의 설계
[1] | Pjk | 2010.06.01 | 24826 |
| 19 |
공작기계의 열변형 대책
[1] | Pjk | 2010.05.28 | 22073 |
| 18 |
신.재생에너지-연료전지
| Pjk | 2010.05.27 | 17006 |
| 17 |
탄소강의 변태-공석강, 아공석강,과공석강
[2] | Pjk | 2010.05.20 | 112736 |
| 16 |
공구 재료 종류와 업계동향
| Pjk | 2010.05.12 | 24857 |
| 15 |
2010년 기계설계산업기사 2회필기 기출문제
| Pjk | 2010.05.10 | 27483 |
| 14 |
2차시스템 : PD제어기
[2] | Pjk | 2010.05.07 | 37567 |
| 13 |
풍력에너지
[1] | Pjk | 2010.05.07 | 21277 |
| 12 |
근궤적(Root Locus)과 설계응용- 근궤적에서 시스템의 안정범위 확인.
| Pjk | 2010.05.02 | 30791 |
| 11 |
재료의성질-공식
| Pjk | 2010.04.29 | 30832 |
| 10 |
30º사다리꼴 나사의 호칭
| Pjk | 2010.04.23 | 32352 |
| 9 |
칩과 공구의 절삭온도분포
| Pjk | 2010.04.21 | 26725 |
| 8 |
Screw Jack (나사잭) 설계
| Pjk | 2010.04.17 | 46797 |
| » |
Matlab을 이용한 - 근궤적작도
| makersweb | 2010.04.09 | 34512 |
| 6 | Hardness Test-경도시험기 측정원리와 특징 및 주의점 | Pjk | 2010.04.02 | 30782 |
| 5 |
Fe-Fe3C 평행상태도
| Pjk | 2010.03.30 | 40079 |
| 4 |
점성계수와점도계종류
| Pjk | 2010.03.30 | 43184 |
| 3 | 차원과 단위의 정의 | Pjk | 2010.03.30 | 28108 |
| 2 | 경도시험기 로크웰, 브리넬, 비커스, 쇼어 경도 환산표 | Pjk | 2010.03.30 | 30877 |
| 1 | 금속재료의 기계적 경도측정 시험법 | Pjk | 2010.03.30 | 22783 |